L’IA, nouvelle alliée des mathématiciens ?
- Des modèles d’IA produisent des raisonnements d’un étudiant en première année de thèse sans pour autant dépasser le niveau des mathématiciens humains.
- De nombreux obstacles, liés aux méthodes de l’IA, induisent des freins dans des domaines de recherche avec des données limitées.
- Malgré tout, sans pour autant fournir des solutions complètes, l’IA peut servir d’assistant traitant plusieurs domaines différents.
- Par exemple, Gauss de Math_inc a formalisé le Théorème des Nombres Premiers fort (PNT) en Lean, avec 25 000 lignes de code et plus de 1 000 théorèmes et définitions.
- À court terme, les chercheurs utiliseront des plateformes pour générer et vérifier des preuves, tandis qu’à long terme, des systèmes pourraient combiner génération automatique et des vérifications formelles.
Les progrès récents du raisonnement automatique placent l’intelligence artificielle au cœur de nouvelles investigations en mathématiques. Des systèmes comme Goedel-Prover, conçus pour générer et valider des preuves formelles, ont montré en 2025 une progression notable en atteignant des niveaux de performance élevés sur des jeux de tests spécialisés1. Dans le même temps, APOLLO a mis en avant la capacité d’un modèle à collaborer avec l’assistant de preuve Lean pour produire des démonstrations vérifiables, tout en révisant automatiquement certaines étapes erronées2.
Les enjeux liés à ces avancées ont été examinés lors de la conférence IA et Mathématiques organisée en avril 2025 par Hi ! PARIS, qui a mis en avant le rôle croissant de la vérification formelle dans les recherches actuelles3. Ces travaux rejoignent certaines analyses publiées dans la presse scientifique. Le Monde a souligné en 2024 le potentiel de ces outils pour accélérer la production de résultats, en évoquant un recours important aux modèles pour sonder des pistes difficiles d’accès par les approches traditionnelles4. De son côté, Science & Vie a rapporté en 2025 que certains systèmes avaient obtenu des scores élevés à des compétitions de type olympiade, ce qui témoigne de leur capacité à traiter des problèmes structurés5, même si ces scénarios ne reflètent que partiellement les exigences de la recherche mathématique.
Pour circonscrire ces dynamiques tout en démêlant le vrai du faux, Amaury Hayat, professeur à l’École des Ponts ParisTech (Institut Polytechnique de Paris), chercheur en mathématiques appliquées et en intelligence artificielle, livre son expertise. Il dirige le projet DESCARTES, consacré aux méthodes d’apprentissage dans des contextes de données rares, ainsi qu’à plusieurs travaux portant sur l’apprentissage par renforcement appliqué à la démonstration automatique. Ses analyses permettent d’examiner les évolutions actuelles du raisonnement automatisé en mathématiques en s’appuyant sur des données, des outils et des résultats publiés.
#1 L’IA peut résoudre tous les problèmes mathématiques ouverts de recherche sans intervention humaine : FAUX
Amaury Hayat. L’intelligence artificielle, notamment les modèles capables de raisonner en langage naturel ou formel, peut déjà produire des preuves au niveau d’un étudiant en thèse de première année dans certains cas. Il existe des situations simples qu’elle ne sait pas encore traiter, mais aussi des problèmes complexes qu’elle peut résoudre.
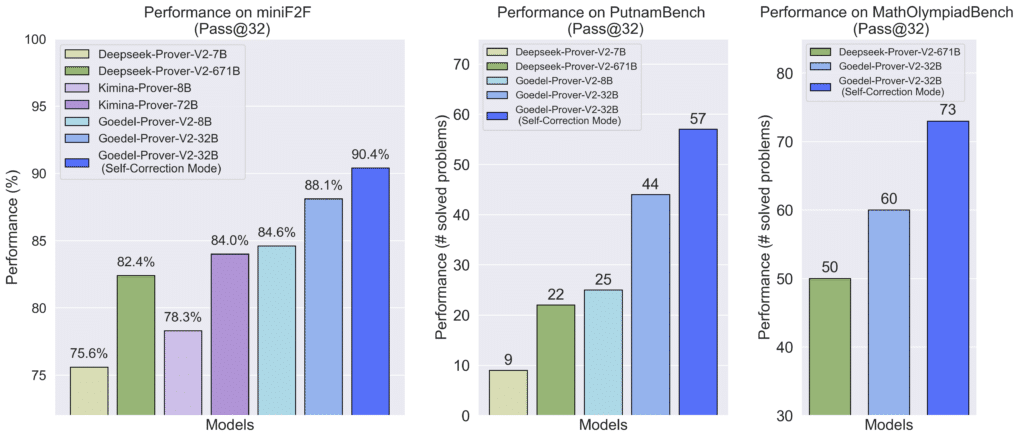
Nous ne disposons pas encore de systèmes capables de générer, du début à la fin, des preuves surpassant le niveau des mathématiciens humains. Cependant, les IA peuvent déjà fournir des preuves très intéressantes et, parfois, résoudre des problèmes restés ouverts depuis longtemps. Dans ces cas, elles exploitent souvent des fragments de solutions éparpillés dans différents articles ou domaines, que l’IA parvient à combiner efficacement grâce à sa capacité à accéder et organiser la connaissance disponible sur Internet. Par exemple (figure 1), GoedelProver‑v2, un modèle formel, a été entraîné sur 1,64 million d’énoncés formalisés et atteint, en 2025, une précision de 88,1 % sans self‑correction et de 90,4 % avec self‑correction sur le benchmark MiniF2F6.
#2 La rareté des données formalisées freine fortement l’entraînement des modèles d’IA : VRAI
Les principaux obstacles sont davantage liés aux méthodes de l’IA qu’aux mathématiques elles-mêmes. Dans des domaines de recherche très spécialisés, les données sont extrêmement limitées. Or, avec les méthodes actuelles d’entraînement des IA, cette rareté constitue un frein important. L’apprentissage par renforcement peut théoriquement pallier ce problème, mais il exige tout de même un nombre significatif d’exemples pour être efficace, et il est surtout pertinent lorsque la vérification automatique est possible.
Aujourd’hui, cette vérification peut se faire soit en langage naturel, ce qui limite les types de problèmes abordables, soit en langage formel, où un ordinateur peut confirmer directement si une preuve est correcte. Le défi est que les IA actuelles qui s’expriment en langage formel ne sont pas encore au niveau des IA qui s’expriment en langage naturel.
Deux axes sont explorés pour progresser : augmenter la quantité de données en traduisant automatiquement du langage naturel vers le langage formel et améliorer les méthodes d’apprentissage par renforcement. Cette approche permet de combiner la puissance des modèles en langage naturel avec la rigueur des vérifications formelles, en fournissant un feedback automatique pour l’entraînement par essais et erreurs.
Godel-Prover est intéressant, car il a rapidement atteint les performances de notre modèle sur le dataset PutnamBench, initialement obtenu avec un nombre très limité d’exemples. Les versions ultérieures, ainsi que DeepSeek-Prover, sont extrêmement performantes, notamment pour des exercices de type olympiade.
Notre objectif avec DESCARTES est différent : nous visons des problèmes de niveau recherche, caractérisés par un régime de faibles données. L’enjeu est donc de développer des modèles capables de travailler dans ces conditions, contrairement aux méthodes classiques qui exploitent de très grandes quantités d’exemples.
#3 L’IA peut servir d’assistant efficace dans la collaboration scientifique : VRAI
Pour la majorité des problèmes que je teste, même les meilleurs modèles ne fournissent pas de solution complète. Cependant, il arrive que l’IA fournisse des réponses intéressantes, et ce, assez régulièrement. Même si ce n’est pas aussi fiable que de consulter un collègue expert, l’avantage est qu’on obtient une interface unique capable de traiter plusieurs domaines simultanément, ce qui fait gagner beaucoup de temps. Parfois, cela équivaut presque à avoir un collègue très expérimenté à disposition pour évaluer ce qui est faisable. Par exemple, Gauss de Math_inc a formalisé le Théorème des Nombres Premiers fort (PNT) en Lean, produisant environ 25 000 lignes de code et plus de 1 000 théorèmes et définitions7, tandis que Prover Agent utilise une boucle de feedback pour générer des lemmes auxiliaires et compléter des preuves8. Ces modèles permettent de réduire considérablement le temps consacré à l’exploration et à la vérification, tout en renforçant la rigueur des résultats.
#4 Les systèmes de calcul avancés comprennent réellement le raisonnement mathématique quand ils produisent des preuves : FAUX
Pour le projet DESCARTES, nous travaillons directement en langage formel, ce qui permet à l’ordinateur de vérifier la correction des preuves. En revanche, lorsque j’utilise des LLM classiques pour des articles mathématiques hors de ce projet, je dois lire et vérifier manuellement les preuves. Cela fait gagner beaucoup de temps, mais il subsiste un risque : les erreurs produites par les modèles sont parfois surprenantes, inattendues, et ne correspondent pas à celles qu’un humain ferait. Elles peuvent parfois paraître très crédibles tout en étant fausses, ce qui nécessite une vigilance particulière.
#5 L’IA risque de remplacer complètement l’enseignement des mathématiques : FAUX
Il faut distinguer deux niveaux dans l’enseignement des mathématiques : la formation jusqu’au niveau master et la recherche post-master. Pour l’apprentissage des bases et la compréhension des preuves, la capacité d’une IA à démontrer des théorèmes ne remet pas fondamentalement en question l’enseignement classique. L’entraînement humain à reproduire des preuves reste essentiel pour développer le raisonnement.
En revanche, dans le cadre de projets de recherche ou d’examens où les étudiants disposent de toutes les ressources, l’IA peut jouer un rôle d’assistant personnel. Par exemple, dans un projet de master, elle pourrait aider à produire des preuves sur des problèmes ouverts, ce qui enrichirait l’expérience d’apprentissage et la créativité des étudiants.
#6 Certains systèmes numériques avancés peuvent générer des articles scientifiques quasi complets, mais leur fiabilité reste variable : INCERTAIN
À court terme, les chercheurs utiliseront des plateformes comme ChatGPT, Gemini ou Mistral pour générer et vérifier des preuves rapidement, gagnant ainsi un temps considérable. Des outils spécialisés commencent également à émerger, comme Google Labs pour explorer Google Scholar ou Alpha Evolve pour la construction de structures mathématiques, tandis que Gemini‑3, Deep Think et GPT-5-pro (modèles de langage) génèrent d’abord une ébauche, puis utilisent, selon les indications disponibles, des outils de vérification pour identifier certaines erreurs éventuelles.
À moyen ou long terme, des systèmes pourraient combiner génération automatique et vérification formelle, accélérant la recherche et influençant les modes de publication et les attentes académiques. Les modèles actuels sont déjà capables de produire des articles presque complets sur la base de publications précédentes, ce qui pourrait transformer la production d’articles “incrémentaux” et libérer du temps pour des recherches plus ambitieuses. Par exemple, des tests comparatifs montrent que sur le benchmark miniF2F, APOLLO atteint 75 % de succès pour les preuves générées automatiquement, alors que Goedel-Prover atteint 57,6 %9. Toutefois, certains modèles peuvent produire des erreurs conceptuelles subtiles ou des passages répétitifs, rendant la supervision humaine indispensable pour valider la fiabilité scientifique.
Il faudra certainement repenser certains aspects de la carrière des chercheurs, notamment le système de publication, la relecture par les pairs et l’écriture des articles. Les modèles sont aujourd’hui capables de produire des preuves et des articles de qualité, et cela pourrait modifier la nature et la fréquence des publications scientifiques.