Satellites: why are ‘Lagrange points’ so important?

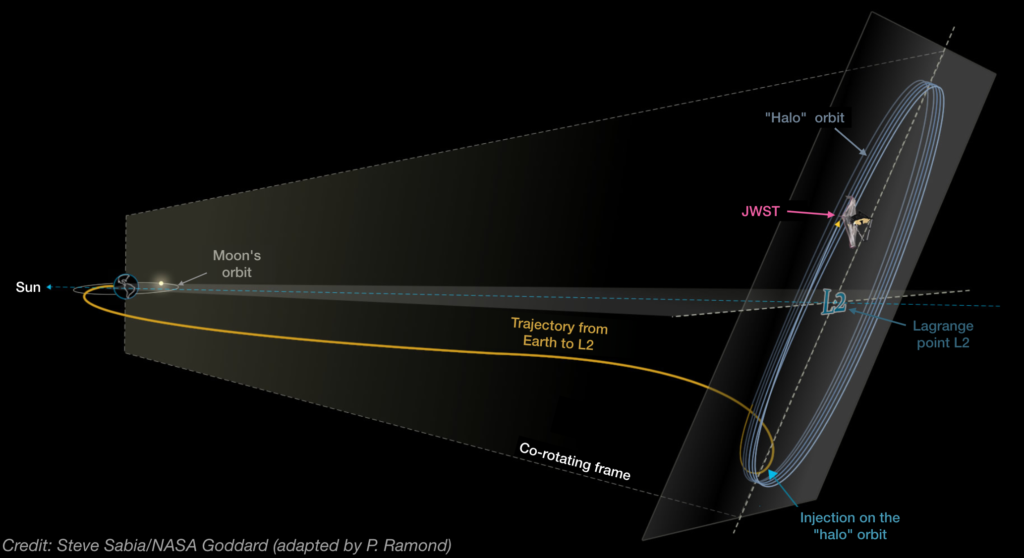
The James Webb Space Tele­scope has arrived safe­ly at its des­ti­na­tion – the famous Lagrange point L2 locat­ed in the inter­plan­e­tary void of our Solar sys­tem, some 1.5 mil­lion kilo­me­tres from Earth. But why there? What is so spe­cial about Lagrange points, of which there are sev­er­al, that space agen­cies have been send­ing satel­lites to for the past 50 years?

Since Isaac New­ton for­mu­lat­ed the laws of mechan­ics and grav­i­ta­tion at the end of the 17^th  Cen­tu­ry, the “three-body prob­lem”, which con­sists of deter­min­ing the motion of three celes­tial objects under their mutu­al grav­i­ta­tion­al attrac­tions, has been one of the most fruit­ful prob­lems of clas­si­cal physics. Attempts to solve it have led to count­less the­o­ret­i­cal advances, which in turn have enabled many rev­o­lu­tion­ary prac­ti­cal appli­ca­tions. Even though we have a much bet­ter under­stand­ing of the prob­lem and its dif­fi­cul­ty, in par­tic­u­lar thanks to the work of Hen­ri Poin­caré at the end of the 19^th Cen­tu­ry, it is not, to this day, com­plete­ly solved.

Lagrange points nat­u­ral­ly appear as spe­cial solu­tions of the so-called ‘restrict­ed’ three-body prob­lem, in which one of the bod­ies is very small com­pared to the oth­er two. This is the case for the motion of a satel­lite around the Sun and a planet.

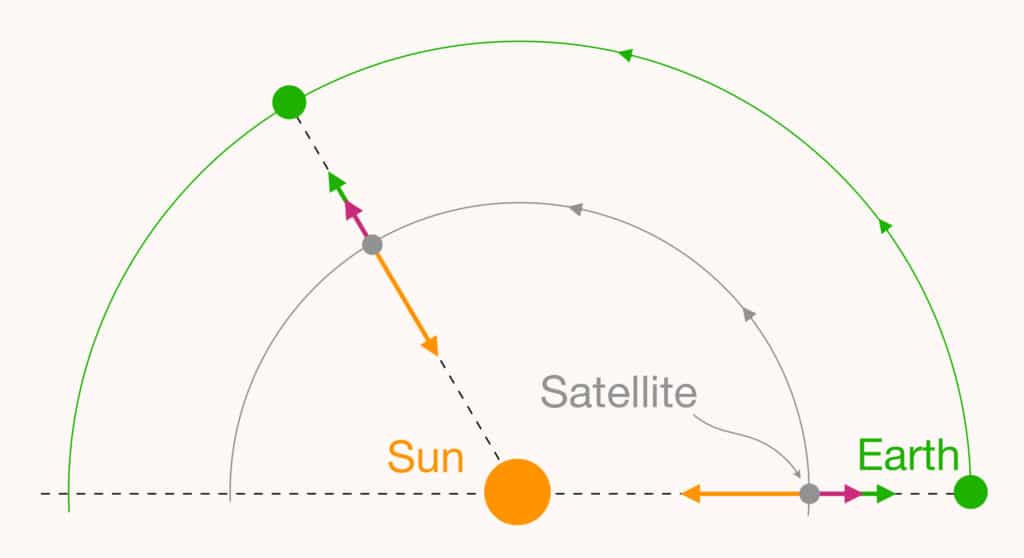
Let us first con­sid­er the orbit of the Earth around the Sun, which is a near-per­fect cir­cle. The Earth makes a com­plete orbit around the Sun in one year, a peri­od known as its rev­o­lu­tion. Let us now imag­ine plac­ing a satel­lite in a cir­cu­lar orbit around the Sun with the the same rev­o­lu­tion (exact­ly one year) and such that it always lies on the Earth-Sun axis. By adjust­ing its dis­tance from the Sun in just the right way, the force of attrac­tion of the Sun will exact­ly com­pen­sate for that of the Earth and the satel­lite will be ‘in equilibrium’.

How­ev­er, the satel­lite is also sub­ject to a cen­trifu­gal force (the one that pulls us out­wards in a mer­ry-go-round). This force adds to the grav­i­ta­tion­al attrac­tions, but does not change the big pic­ture: we can always adjust the posi­tion of the satel­lite on the Sun-Earth axis so that the three forces can­cel one anoth­er, as shown in the fig­ure below.

The orbit that we have just con­struct­ed for the satel­lite is pre­cise­ly what astronomers call a ‘Lagrange point’. But why Lagrange ‘point’ and not ‘orbit’? The rea­son lies in anoth­er way of look­ing at our prob­lem. Indeed, since the satel­lite and the Earth orbit the Sun in a year, we can imag­ine orbit­ing with them, and take this rev­o­lu­tion into account in the graph­ic rep­re­sen­ta­tion of the prob­lem. The satel­lite’s tra­jec­to­ry is then reduced to a point, placed between the Sun and the Earth, which is also fixed in this so-called ‘co-turn­ing’ ref­er­ence frame. This point, which in fact rep­re­sents an orbit, is the Lagrange point L1.

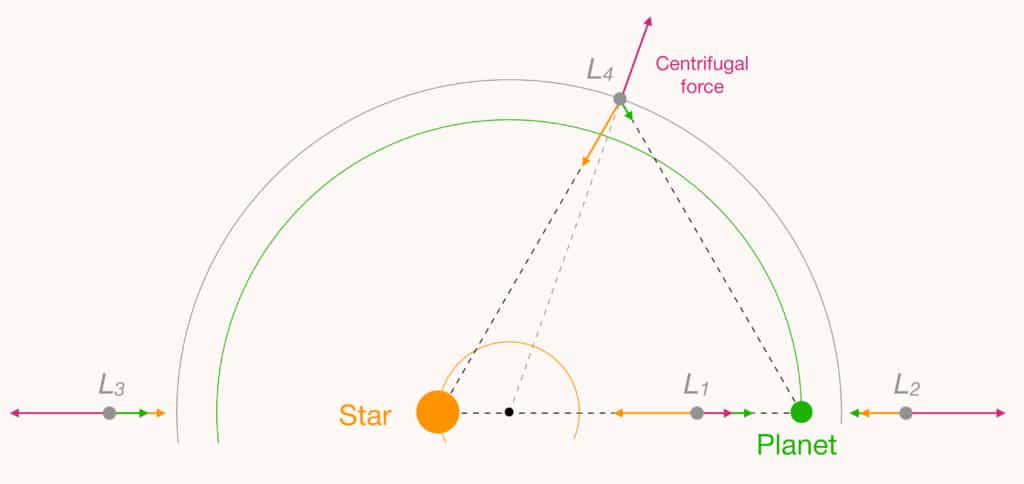
The co-turn­ing ref­er­ence frame is very use­ful and allows us to uncov­er four addi­tion­al Lagrange points, by sim­ply look­ing for oth­er spots where all three forces (Earth and Sun’s attrac­tion and the cen­trifu­gal force) can­cel out. Two of these points, called L2 and L3, are also on the Sun-Earth axis, as shown in the fig­ure below.

The Lagrange point L2 lies on the oth­er side of the Earth from L1, and L3 on the oth­er side of the Sun. It is clear from the fig­ure that the three forces expe­ri­enced by a satel­lite at these points can­cel out: this is why they are also called ‘equi­lib­ri­um points’. Togeth­er with L1, the points L2 and L3 cor­re­spond to three exact solu­tions of the three-body prob­lem deter­mined by Leonard Euler and pub­lished in 1765. Locat­ed at the oppo­site end of the Sun from us, the point L3 has been the sub­ject of many flights-of-fan­cy since ancient times. One of these is a hypo­thet­i­cal ‘anti-Earth’, which would exist at L3 but which would be exact­ly hid­den from us by the Sun.

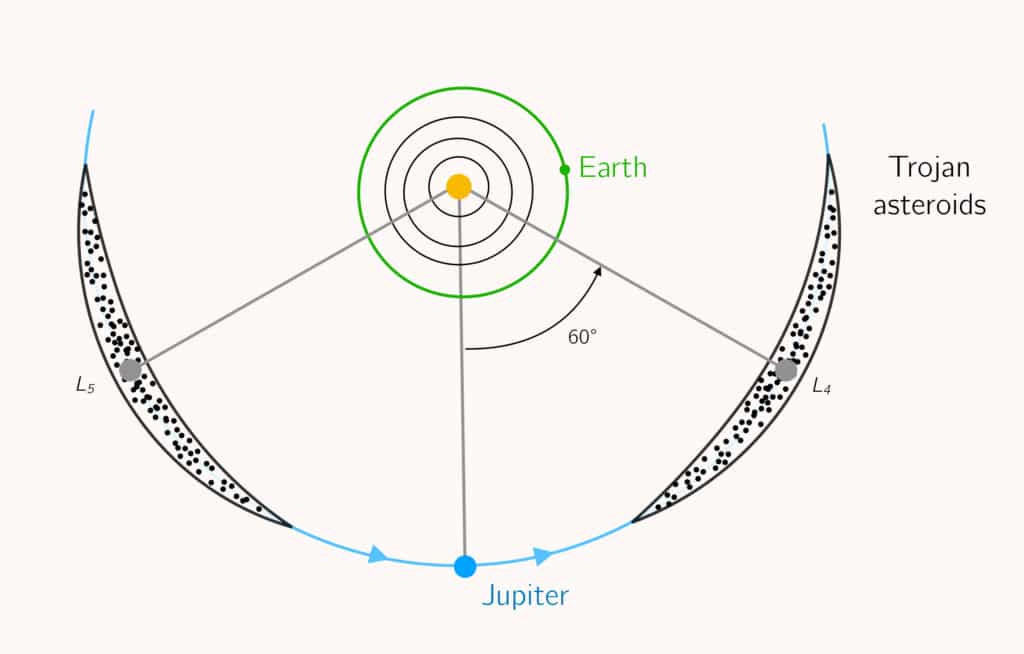
It was Joseph-Louis Lagrange who showed in 1772 that two oth­er points, L4 and L5, exist. These are not on the Sun-Earth axis, but locat­ed at equal dis­tance from both, so as to make an equi­lat­er­al tri­an­gle. At these points, the two grav­i­ta­tion­al forces and the cen­trifu­gal force, although not aligned, still can­cel out exact­ly, as shown in the fig­ure below. In prac­tice, the satel­lite is there­fore almost on the Earth­’s orbit, 60° ahead of (L4) or behind (L5) it.

Since Lagrange points are asso­ci­at­ed with equi­lib­ri­um posi­tions, it would not be sur­pris­ing to find nat­ur­al objects (such as small aster­oids) at these loca­tions in the Solar sys­tem. In the case of the Sun-Jupiter sys­tem, about 10 000 aster­oids have been observed to date around the L4 and L5 Lagrange points. Called Tro­jan aster­oids, some of these even have nat­ur­al satel­lites of their own, such as the largest called ‘(624) Hec­tor’ and its aster­oidal moon “Sca­man­drios”.

These thou­sands of objects are proof that the Lagrangian sta­bil­i­ty regions are real and not just the­o­ret­i­cal. In fact, most plan­ets of the Solar sys­tem have Tro­jan aster­oids, that is,  small rocky bod­ies locat­ed near the L4 and L5 loca­tions of the cor­re­spond­ing Sun-plan­et sys­tem. How­ev­er, one mys­tery remains, as no Tro­jans have ever been observed for the Earth-Sat­urn sys­tem. It is sus­pect­ed that grav­i­ta­tion­al dis­tur­bances cre­at­ed by Jupiter pre­vent aster­oids from stay­ing there too long⁴. Yet, iron­i­cal­ly, two of Sat­urn’s nat­ur­al satel­lites, Tethys and Dionne, have Tro­jans themselves!