Einstein thought that black holes didn’t exist, but (indirect) observations in the 2010s proved him wrong: black holes are real. Here we take a look at a century of black holes, from Schwarzschild’s first calculations to the recent research findings from Szeftel and Klainerman.
Cosmic gluttons
Historically, black holes were initially mathematical objects, unexpected by-products of the theory of general relativity. This theory, published in 1915 by Albert Einstein, revolutionised our conception of gravitation and space. As such, space and time form a continuum that has its own geometry. In particular, space-time can bend under matter, like a sheet supporting a heavy object. To describe this curvature, Einstein formulated an equation that today bears his name:
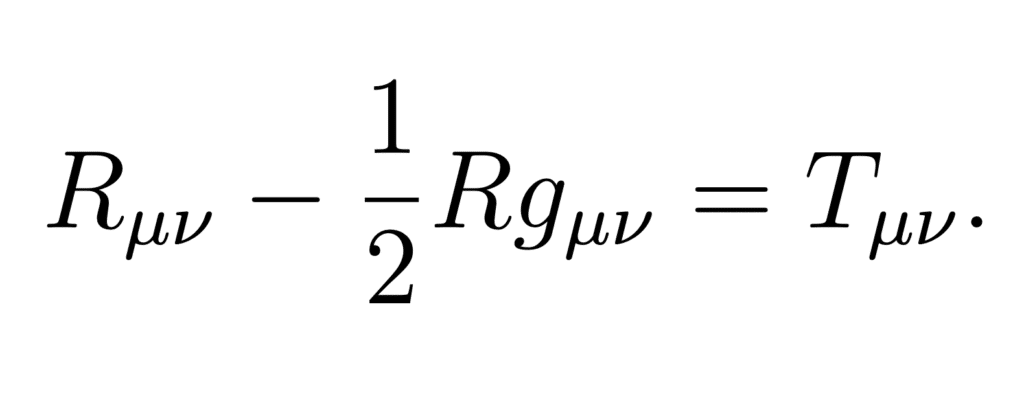
Just a few months after this publication, the German physicist Karl Schwarzschild, then serving on the Russian front in the Great War, discovered a particular solution to Einstein’s equations. Called the Schwarzschild metric, it describes space-time in the vicinity of a spherically symmetric body, such as a star or a planet. If the density of the body exceeds a certain threshold, it is a black hole. The density of such an object is simply insane: to turn the Earth into a black hole, you would have to fit it into a pistachio! Black holes are so dense that nothing can escape them: once they pass their boundary, or event horizon, any object will remain trapped forever. This also applies to light! Black holes therefore do not emit any light, hence their name.
How do we observe them?
Problem: all our astronomical observations are based on the study of light coming from the cosmos, collected by telescopes or simply our eyes. To observe black holes, you therefore have to be cunning!
One solution is to detect gravitational waves rather than light waves. Another spectacular prediction of general relativity, gravitational waves are the trace of cataclysmic phenomena such as the fusion of two black holes in space-time. They propagate at the speed of light and we can detect their motion thanks to the giant LIGO-VIRGO collaboration interferometers. These kilometre-scale detectors allowed for the first indirect observation of black holes in 2015.
The first photograph of a black hole was taken in 2019. Here, it was not the black hole itself that was observed but the disc of glowing matter ready to be devoured orbiting the giant star.

Uncertain birth
Long before indirect observation could even be envisaged, mathematics was the best tool for tackling the mysteries surrounding black holes. An important question was: how do black holes form? What mechanism can possibly allow for such monsters?
To answer this, the physicist/mathematician Roger Penrose put forward a singularity formation theorem in the 1960s1. This states that the causally catastrophic singularity at the centre of black holes necessarily forms if spacetime locally satisfies very strong curvature conditions. Such conditions can be met during the gravitational collapse of a star at the end of its life, when it has used up all its fuel. This work earned Penrose the 2019 Nobel Prize in Physics, and led to the understanding that the death of a star can give rise to the birth of a black hole.
A conjecture becomes a theorem
Technical progress in modern astronomy allows us to observe stars that are further and further away, and thus probe their past. We can therefore hope to observe the birth, or at least the young lives, of black holes. But another important question eludes our telescopes: the future of black holes. In particular, are they stable?
In physics, we prefer stable objects to unstable ones. Imagine a ball on top of a hill: if you push it slightly, it will roll down the hill! The top of the hill is therefore an unstable position and it is sensitive to small perturbations. In contrast, the bottom of a hill can be thought of as being a stable position. The James Webb Space Telescope (JWST) will perfectly illustrate these concepts: its destination is the Lagrange point L2, which is stable to angular perturbations, but unstable to radial ones…

We formulate the stability of black holes as follows: what happens to a Schwarzschild solution representing a black hole if we slightly disturb it? Does it return to equilibrium like the ball at the bottom of a hill? Yes, according to two new long articles23 by mathematicians Jérémie Szeftel and Sergiu Klainerman. The result of ten years of research, their demonstration is based on a detailed understanding of the geometry of black holes, as well as on the development of numerous techniques for analysing partial differential equations.
The final state of our universe
Szeftel and Klainerman’s resolution of the stability conjecture for black holes is a major mathematical achievement, but their work is by no means the end of the story – quite the contrary. Their ultimate goal is known as the final state conjecture. In simple terms, this states that in the extremely distant future, the universe will consist only of black holes moving away from each other. In this scenario, if two black holes are too close, they will merge, liberating gravitational waves.
Mathematically proving this conjecture requires solving many intermediate questions, including the black hole stability conjecture. Indeed, if all the contents of our universe eventually converge to black holes, the black holes must “converge to themselves”, that is, they become stable! Another ‘subconjecture’ is that of cosmic censorship, introduced by Penrose in 1969, which predicts that singularities such as those found at the centre of black holes cannot be ‘naked’, that is, exist without an event horizon around them that protects the universe from their paradoxical nature. The final state conjecture and most of its ‘subconjectures’ are currently completely out of reach. They will no doubt keep mathematicians busy for decades, if not hundreds of years to come.
To find out more
Voyage au Coeur de l’Espace-Temps, Stéphane d’Ascoli et Arthur Touati (2021), First Editions







