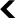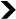A (very) brief history of infinity

Once consi­de­red as a sacred concept (only God is infi­nite) or a meta­phy­si­cal one (the human mind will never be able to enti­re­ly conceive it), infi­ni­ty has since ente­red the domain of science and tech­no­lo­gy. Today, we mea­sure it, com­pare it, stu­dy it, and use it almost like a nor­mal number.

But what is infi­ni­ty ? And how did we learn to tame it ?

It seems that ques­tions about infi­ni­ty are almost as old as huma­ni­ty. Unfor­tu­na­te­ly, the wri­tings that attest to this are all the rarer because they are old. We know that the phi­lo­so­phers of the first mil­len­nium B.C. were alrea­dy won­de­ring about the ama­zing pro­per­ties of infinity.

But is infi­ni­ty only a concept ? A weird idea that mathe­ma­ti­cians play with ? Or does it have a connec­tion with the world around us ? Is any­thing real­ly infi­nite ?

For Anaxi­man­der, infi­ni­ty is the foun­ding prin­ciple of rea­li­ty. From it are born an infi­nite num­ber of worlds that fill the volume of the Uni­verse. For Hera­cli­tus, on the other hand, it is time that is infi­nite. It has always been and will always be. It is through infi­ni­ty that we per­ceive our own existence.

Of course, none of these sta­te­ments are sup­por­ted by an “expe­riment” or a “mea­su­re­ment” by cur­rent scien­ti­fic stan­dards. It is more a phi­lo­so­phi­cal posi­tion that dif­fe­ren­tiates one school of thought from another.

Of course, infi­ni­ty is first and fore­most a mathe­ma­ti­cal concept. And it is mathe­ma­ti­cians who took it upon them­selves to observe it a lit­tle clo­ser. Zeno of Elia (~450 BC) tried to show the “phy­si­cal” impos­si­bi­li­ty of infi­ni­ty, not by mea­su­ring it but by using it to divide things into smal­ler and smal­ler elements.

The result is his famous “arrow para­dox” that, accor­ding to him, should never be able to hit its tar­get. Indeed, one can always divide its remai­ning path by two and there will always remain a por­tion of path to cover (1/2, 1/4, 1/8, 1/16, 1/32), ad infi­ni­tum.

Since it takes an infi­nite num­ber of steps to cross the dis­tance bet­ween the bow and the tar­get, Zeno conclu­ded that it was impos­sible for the arrow to reach its des­ti­na­tion in a finite time.

Howe­ver, this para­dox was sol­ved much later by one of the branches of mathe­ma­tics that stu­dies infi­nite sums of num­bers : the series.

Adding 1/2+ 1/4+ 1/8+ 1/16+… is like adding 1/2+ 1/2²+ 1/2³+ 1/2⁴+…

This series is cal­led a geo­me­tric series. It is writ­ten in the form : 

Its reso­lu­tion is very simple. When n tends to infi­ni­ty, the value of this sum tends natu­ral­ly to 1.

A sche­ma­tic reso­lu­tion is even sim­pler. In the figure below, we can intui­ti­ve­ly see that, to fill a square with side 1, we must add the ele­ments whose area cor­res­ponds exact­ly to the series above it.

What Zeno was mis­sing was the coun­te­rin­tui­tive result that the sum of an infi­nite num­ber of num­bers does not always give an infi­nite result.

In other words, it is not because the tra­jec­to­ry of the arrow can be decom­po­sed into an infi­nite num­ber that the time it will take to cover them will be infi­nite. Para­dox sol­ved. The arrows can now reach their tar­get with com­plete peace of mind.

Later, Isaac New­ton per­fec­ted the art of mea­su­ring arbi­tra­ri­ly small values by deve­lo­ping infi­ni­te­si­mal cal­cu­lus. This led to the famous deri­va­tives (and inte­gers) which mathe­ma­tics, but also modern phy­sics, could not do without today to des­cribe and unders­tand the world.

There is no need to unders­tand or visua­lise infi­ni­ty to use it. In the end, infi­ni­ty is just a tool among many others that mathe­ma­tics puts at our dis­po­sal to mea­sure, cal­cu­late and unders­tand our environment.

But a Ger­man mathe­ma­ti­cian from the end of the 19^th Cen­tu­ry went much fur­ther than anyone else at the time to mani­pu­late infi­ni­ty, or more pre­ci­se­ly infi­nite sets.

Georg Can­tor asked him­self a simple ques­tion : can we com­pare two infi­nite sets ? Can one be “big­ger” than the other ?

His ans­wer lies in the way he com­pares two sets : ins­tead of coun­ting the num­ber of ele­ments of the lat­ter and com­pa­ring them (which can­not be done with an infi­nite set), the method consists in trying to match an ele­ment of the first set with an ele­ment of the second. If each ele­ment finds its part­ner and none remains alone (we call this a bijec­tion), we can then say that the two sets are equal. And this method applies to both finite and infi­nite sets.

This is how we can prove that the size of the (infi­nite) set of posi­tive inte­gers is strict­ly equal to that of the set of inte­gers (posi­tive and negative).

What’s more, we can also show that, although there are infi­ni­te­ly many frac­tions bet­ween two inte­gers, the size of the set of inte­gers is strict­ly equal to the size of the set of num­bers that are writ­ten as frac­tions. Howe­ver, it has also been pro­ven that the set of real num­bers (all num­bers writ­ten with a deci­mal point and a finite or infi­nite num­ber of deci­mal places) is strict­ly lar­ger than the set of integers.

As coun­ter-intui­tive as it may seem, two dif­ferent infi­ni­ties can have the same size, but, conver­se­ly, not all infi­ni­ties are equal.

Can we draw figures with infi­nite parameters ?

Besides the circle (which can be consi­de­red as a poly­gon with an infi­nite num­ber of sides), other strange figures star­ted to emerge during the second half of the 20^th Cen­tu­ry : fractals.

One way to create them is to build them by ite­ra­tion, step by step. After an infi­nite num­ber of steps, the figure is fini­shed, and we can stu­dy its pro­per­ties. The Von Koch flake, for example, is an extra­or­di­na­ry figure : although its sur­face is finite, its per­ime­ter is infinite.

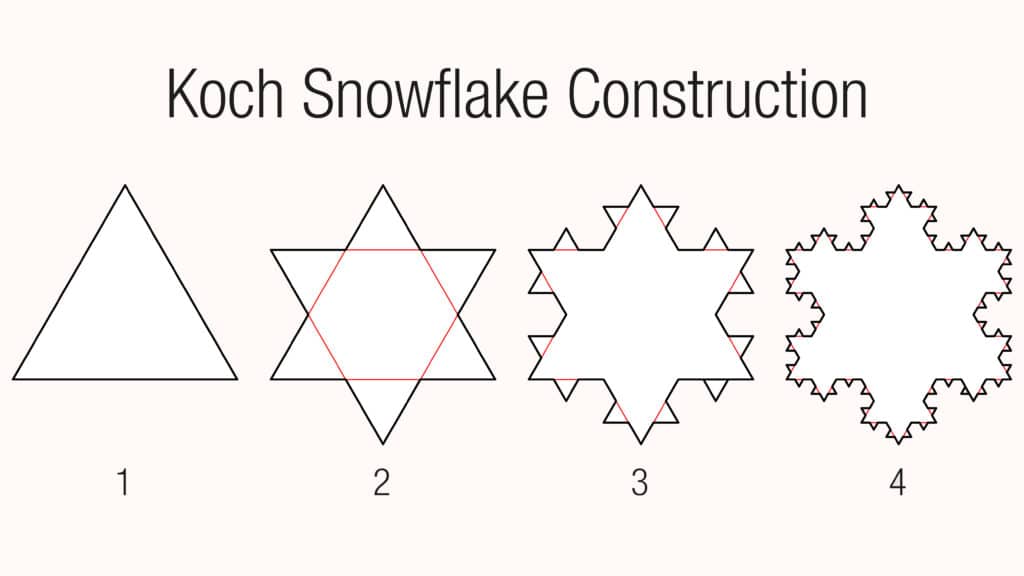
This kind of geo­me­try has been suc­cess­ful­ly applied in the field of tele­com­mu­ni­ca­tions. Since the end of the 80’s, frac­tal anten­nas have been deve­lo­ped, whose length, if not infi­nite, is very large, but whose volume remains small, which allows to obtain com­pact and effi­cient systems.