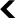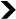Peut-on quantifier la beauté ?
Pourquoi certaines images sont-elles appréciées de manière consensuelle ? Quelles propriétés et règles sous-jacentes déterminent cette préférence ? Des physiciens de l’École polytechnique en collaboration avec la galerie ArtInResearch apportent des éléments de réponse dans une récente publication1 en s’inscrivant dans un domaine à la croisée des disciplines : « l’esthétique quantitative ».
Une vision universaliste de la beauté.
“Le beau est ce qui plaît universellement, sans concept” Emmanuel Kant2
Le concept de beauté, considéré comme une propriété universelle et intrinsèque d’un objet, apparaît dans de nombreuses contributions artistiques, elles-mêmes ancrées dans toutes les périodes historiques. De la Grèce antique à la Renaissance, de l’architecture à la peinture, cette quête de l’idéal a souvent convergé vers l’établissement de règles précises de représentation. Ces règles, parfois très quantitatives, peuvent se matérialiser sous plusieurs aspects au sein des œuvres : proportions des corps pour les sculptures ; répartitions des actes et dialogues au théâtre ; symétries en architectures, et bien d’autres exemples. Même pour les œuvres contemporaines qui s’inscrivent dans la continuité de ces disciplines historiques, ces règles subsistent et en constituent d’ailleurs les premiers enseignements académiques.
L’ordre et le chaos
“Total chaos is disquieting. Too much regularity is boring. Aesthetics is perhaps the territory in-between.” Jean-Philippe Bouchaud3
Pourtant, on ne peut s’empêcher de penser à ces œuvres marquantes qui présentent au moins une transgression sensible de ces règles. Combien d’actes et de décors y a‑t-il dans le Cyrano de Bergerac d’Edmond Rostand ? Quel niveau de déstructuration y a‑t-il dans le Guernica de Picasso ? D’une certaine manière, l’œuvre puissante n’est-elle pas celle qui nous transporte entre les règles et leur rejet, le connu et l’inconnu, l’ordre et le chaos ?
Quoi de plus parlant alors pour des chercheurs en physique statistique, où les concepts comme la rupture soudaine de symétrie, la criticalité et l’instabilité sont au cœur de la discipline ?
L’entropie comme mesure du désordre.
Du point de vue de la physique, l’ordre et le désordre sont des notions familières. Un aimant est constitué d’un nombre presque infini de micro-aimants, tous alignés et ordonnés. Mais il suffit d’augmenter la température au-delà de la « température de Curie » pour que cet ordre se brise, que les micro-aimants deviennent indépendants et que l’aimantation globale soit perdue. La mesure de ce désordre et de cette rupture de symétrie est l’entropie, une grandeur fondamentale en thermodynamique. Plus formellement, l’entropie est le nombre de manières d’organiser un système pour qu’il garde les mêmes propriétés physiques. Il y a de nombreuses façons de créer le désordre, mais peu de manières de construire l’ordre.
Une expérience simple sur la préférence visuelle
Au cours de nos recherches, nous avons donc posés la question suivante : existe-t-il une valeur d’entropie pour des classes d’images abstraites simples qui maximiserait leurs qualités esthétiques ?

Pour répondre à cette question, nous avons d’abord généré deux classes d’images abstraites bien réparties sur trois mesures connues de désordre : la dimension fractale ; la compressibilité algorithmique ; et la distribution de la taille des motifs au sein d’une image. Chacune de ces classes d’images passe de l’état ordonné (à gauche) à l’état désordonné (à droite). Nous avons ensuite réalisé des expériences de sondage afin de déterminer quelles images étaient les plus appréciées, d’abord avec l’aide de nos confrères (LadHyX, CFM, ENSAE), puis par le biais de plateformes de diffusion adaptées (Amazon MkTurk). Au total, près de 1000 personnes ont participé aux différentes expériences. Les résultats confirment alors l’intuition : les images (a4,b4) obtiennent les meilleurs scores.
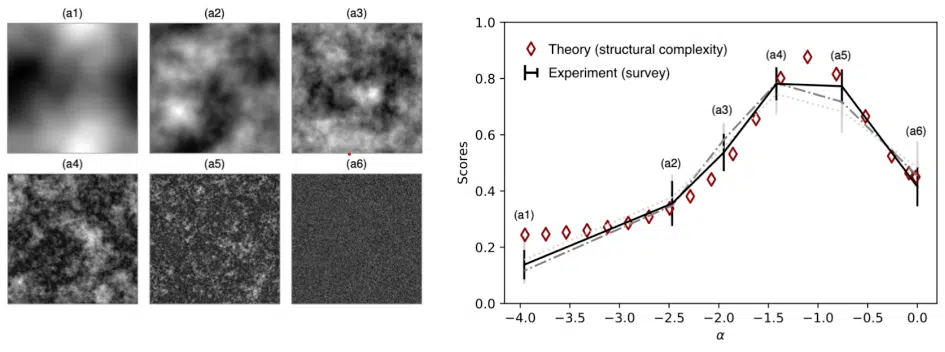
Entropie et complexité structurelle
Intuitivement, les valeurs d’entropies extrêmes ont donc tendance à nous ennuyer ou à nous perdre. À l’inverse, les valeurs intermédiaires captent notre attention en maximisant la présence de structures intéressantes, de motifs intelligibles qui rendent l’image unique. D’une certaine manière, notre cerveau reconnaît les formes et les motifs tout en « gommant » le bruit inutile. Pour simuler ce mécanisme, nous avons ensuite proposé une mesure de « complexité structurelle » (en rouge sur la figure 2) mettant en évidence ces structures. Nous obtenons alors un second résultat : les images d’entropie intermédiaire présentent, en effet, la plus grande complexité structurelle. Il est à noter que les images naturelles, telles que les photographies de forêts ou de paysages, présentent une entropie (statistiquement condensée) autour de cette même valeur intermédiaire.
Une contribution dans un domaine en essor : l’esthétique quantitative.
Aujourd’hui, nos appareils photo, nos logiciels de retouche et même nos moteurs de recherche bénéficient tous des contributions récentes en esthétique quantitative45. Cette discipline, en combinant banques de données massives6, méthodes de traitement d’images et architectures d’apprentissage de pointe7, a permis d’améliorer significativement la notation et la classification automatique des images. Cependant, malgré la performance de ces outils, on peut regretter leur incapacité à fournir des éléments de compréhension sur les mécanismes réels de l’appréciation. Ce sont, en quelque sorte, des automates dont les règles nous échappent.
Notre travail, même s’il s’inscrit dans une même démarche prédictive, s’attache à remettre au centre l’interprétabilité des résultats. Une approche fondamentalement physique en somme.